Calcul de la taxe
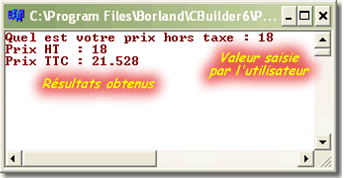
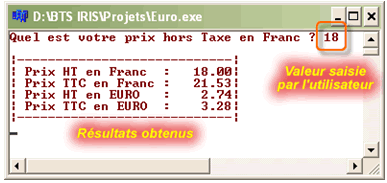
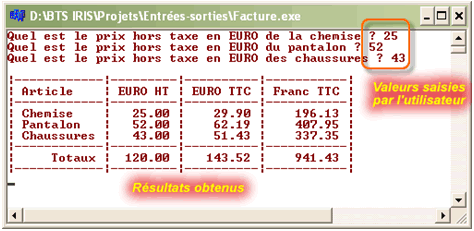
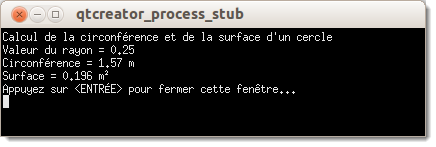
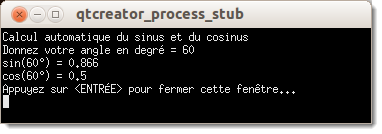
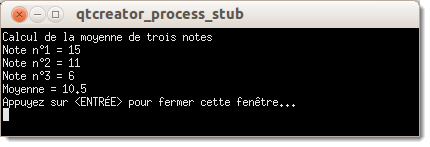
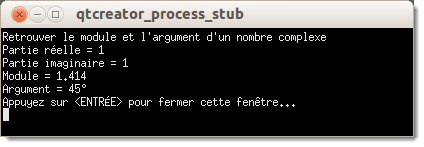
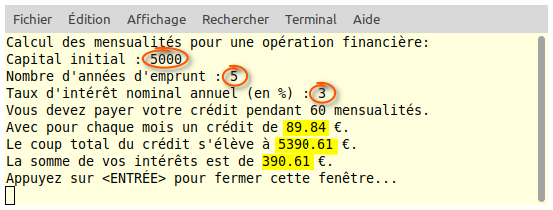
Ce programme permet de calculer le prix avec les taxes. Une fois que le programme est lancé, l'utilisateur devra saisir une valeur quelconque sans les taxes.
- Avant de commencer à coder, identifiez les éléments qui vous paraissent modifiables, c'est-à-dire, susceptible de varier lorsqu'on relance le programme de nouveau.
- De la même façon, identifier les éléments qui vous paraissent au contraire ne pas varier quel que soit le nombre de fois que l'on exécute le programme.
- Identifier donc pour ce programme l'ensemble des variables et des constantes nécessaires à l'édition correcte de ces calculs. Proposez des noms judicieusement choisis.